Context
Zero-knowledge proofs were first conceived in 1989 by Shafi Goldwasser, Silvio Micali, and Charles Rackoff in their paper "The Knowledge Complexity of Interactive Proof-Systems"
Together with a paper by László Babai and Shlomo Moran, this landmark paper invented interactive proof systems, for which all five authors won the first Gödel Prize in 1993.
assuming the existence of unbreakable encryption, one can create a zero-knowledge proof system for the NP-complete graph coloring problem with three colors. Since every problem in NP can be efficiently reduced to this problem, this means that, under this assumption, all problems in NP
assuming one-way functions or unbreakable encryption, that there are zero-knowledge proofs for all problems in IP = PSPACE, or in other words, anything that can be proved by an interactive proof system can be proved with zero knowledge.
Not liking to make unnecessary assumptions, many theorists sought a way to eliminate the necessity of one way functions. One way this was done was with multi-prover interactive proof systems (see interactive proof system), which have multiple independent provers instead of only one, allowing the verifier to "cross-examine" the provers in isolation to avoid being misled.
It can be shown that, without any intractability assumptions, all languages in NP have zero-knowledge proofs in such a system
The property of witness-indistinguishability is related to that of zero-knowledge, yet witness-indistinguishable protocols do not suffer from the same problems of concurrent execution.
Non-interactive zero-knowledge proofs. Blum, Feldman, and Micali showed that a common random string shared between the prover and the verifier is enough to achieve computational zero-knowledge without requiring interaction.
Illustrative Examples
- 2 Balls and A Color Blind Friend
- You know the color of the ball
- The color-blind friend knows if they switched the balls
- You prove the balls are differently colored.
- The Strange Cave of Ali Baba
Details
-
Three critical properties that any zero knowledge proof must satisfy:
- Completeness: If the Prover is honest, then she will eventually convince the Verifier.
- Soundness: The Prover can only convince the Verifier if the statement is true.
- Zero-knowledge: The Verifier learns no information beyond the fact that the statement is true.
-
The Players: Prover, Verifier, Simulator and Extractor.
-
Soundness To prove soundness for a proof of knowledge, we must show that an Extractor exists for every possible Prover. Where:
A knowledge extractor (or just 'Extractor' for short) is a special type of Verifier that interacts with a Prover, and — if the Prover succeeds in completing the proof — the Extractor should be able to extract the Prover's original secret.
Of course this again seems totally contradictory to the purpose of a zero knowledge protocol — where we're not supposed to be able to learn secrets from a Prover. Fortunately we've already resolved this conundrum once for the case of the Simulator. Here again, we take the same approach. The Extractor is not required to exist during a normal run of the protocol. We simply show that it exists if we're allowed to take special liberties with the Prover — in this case, we'll use 'rewinding' to wind back the Prover's execution and allow us to extract secrets.
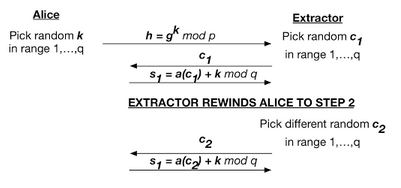
The key observation here is that by rewinding Alice's execution, the Extractor can 'trick' Alice into making two different proof transcripts using the same k. This shouldn't normally happen in a real protocol run, where Alice specifically picks a new k for each execution of the protocol.
If the Extractor can trick Alice into doing this, then he can solve the following simple equation to recover Alice's secret:
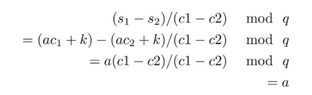
If you ever accidentally use the same k for two different runs of the protocol, an attacker may be able to recover your secret key! This can happen if you use a bad random number generator.